题目内容
（请给出正确答案）
问题描述:给定一个赋权无向图G=(V,E),每个顶点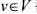
都有权值w(v).如果
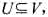,且对任意(u,V)∈E有u∈U或v∈U,就称U为图G的一个顶点覆盖.G的最小权顶点覆盖是指G中所含顶点权之和最小的顶点覆盖.
算法设计:对于给定的无向图G,设计一个优先队列式分支限界法,计算G的最小权顶点覆盖.
数据输入:由文件input.txt给出输入数据.第1行有2个正整数n和m,表示给定的图G有n个顶点和m条边,顶点编号为1,2,...,n.第2行有n个正整数表示n个顶点的权.接下来的m行中,每行有2个正整数u和v,表示图G的一条边(u,v).
结果输出:将计算的最小权顶点覆盖的顶点权值和以及最优解输出到文件output.txt.文件的第1行是最小权顶点覆盖顶点权之和;第2行是最优解xi(1≤i≤n),xi=0表示顶点i不在最小权顶点覆盖中,xi=1表示顶点i在最小权顶点覆盖中.
答案
更多“问题描述:给定一个赋权无向图G=（V,E),每个顶点都有权值w（v).如果,且对任意（u,V)∈E有u∈U或v∈U,”相关的问题
第1题
问题描述:给定一个无向图G=(V.E),设
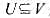是G的顶点集.对任意
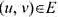,若u∈U且v∈V-U,就称(u,1)为关于顶点集U的条割边.顶点集U的所有割边构成图G的一个割.G的最大割是指G中所含边数最多的割.
算法设计:对于给定的无向图G,设计一个优先队列式分支限界法,计算G的最大割.
数据输入:由文件input.txt给出输入数据.第1行有2个正整数n和m,表示给定的图G有n个顶点和m条边,顶点编号为1,2,...,n.接下来的m行中,每行有2个正整数u和y,表示图G的一条边(u,v).
结果输出:将计算的最大割的边数和顶点集U输出到文件output.txt.文件的第1行是最大割的边数;第2行是表示顶点集U的向量x(1≤i≤n),x=0表示顶点i不在项点集U中,x=1表示顶点i在顶点集U中.
第2题
图的m着色问题描述如下:给定无向连通图G和m种不同的颜色.用这些颜色为图G的各顶点着色,每个顶点着一种颜色.如果有一种着色法,使G中每条边的2个顶点着不同颜色,则称这个图是m可着色的.图的m着色问题是对于给定图G和m种颜色,找出所有不同的着色法.
算法设计:对于给定的无向连通图G和m种不同的颜色,计算图的所有不同的着色法.
数据输入:由文件input.txt给出输入数据.第1行有3个正整数n,k和m,表示给定的图G有n个项点和k条边,m种颜色.顶点编号为1,2,...,n接下来的k行中,每行有2个正整数u、v,表示图G的一条边(u,v).
结果输出:将计算的不同的着色方案数输出到文件output.txt.
第4题
设有一个带权有向图G=(V，E)，w是G的一个顶点，w的偏心距定义为：max(从u到w的最短路径长度
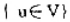其中的路径长度指的是路径上各边权值的和，将G中偏心距最小的顶点称为G的中心，试设计一个函数返回带权有向图的中心(如有多个中心，可任取其中之
参数表中的引用型参数biasdist返回最小偏心距的值，函数返回该中心的顶点号。
第5题
点到某一指定顶点v的最短路径，例如，对于图8-47(a)所示的带权有向图，用该算法求得的从各顶点到顶点2的最短路径如图8-47(b)所示.
关于最短路径的读法以顶点0为例，在从顶点0到顶点2的最短路径上，顶点0的后继为顶点1(即path[0]=1)，顶点1的后继为顶点3(即path[1]=3)，顶点3的后继顶点为2(即path[3]=2).
编写一个算法，求解一个带权有向图的单目标最短路径问题。假设图G的顶点数据的类型为char，边上权值的数据类型为float。
第6题
问题描述:给定一棵有向树T,树T中每个顶点u都有一个权w(u),树的每条边(u,v)也都有一个非负边长d(u,v).有向树T的每个顶点u可以看作客户,其服务需求量为w(u).
每条边(u,v)的边长d(u,v)可以看作运输费用.如果在顶点u处未设置服务机构,则将顶点u处的服务需求沿有向树的边(u,v)转移到顶点v处服务机构所需付出的服务转移费用为w(u).d(u,v).树根处已设置了服务机构,现在要在树T中增设k处服务机构,使得整棵树T的服务转移费用最小.
算法设计:对于给定的有向树T,计算在树T中增设k处服务机构的最小服务转移费用.数据输入:由文件input.txt给出输入数据.第1行有2个正整数n和k.n表示有向树T的边数,k是要增设的服务机构数.有向树T的顶点编号为0,1,...,n.根结点编号为0.在接下来的n行中,每行有表示有向树T的一条有向边的3个整数.第i+1行的3个整数wi、vi、di,分别表示编号为i的顶点的权为wi,相应的有向边为(i,vi),其边长为di.
结果输出:将计算的最小服务转移费用输出到文件output.txt.
第8题
不相交的子集A和B=V-A，并且这两个子集具有下列性质：
(a)A中任何两个顶点在G中都不是相互邻接的;(b)B中任何两个顶点在G中都不是相互邻接的。例如，图8-34就是二部图。对V(G)的一个划分可能是A=(0，3，4，6)和B=(1，2，5，7).
(1)试编写一个算法，判断图G是否是二部图。如果图G是二部图，则你的算法应当把项点划分成为具有上述性质的两个互不相交的子集A和B。证明：当用邻接表表示图G时，这个算法的复杂度可以做到O(n+e)。其中n是图G的顶点个数，e是边数。
(2)证明：任何-棵树都是二部图
(3)证明：当且仅当图G不包含奇数条边的回路时.它是二部图。
第10题
行深度优先搜索，得到的顶点序列是()。
A、a,b,e,c,d,f
B、a,c,f,e,b,d
C、a,e,b,c,f,d
D、a,e,d,f,c,b
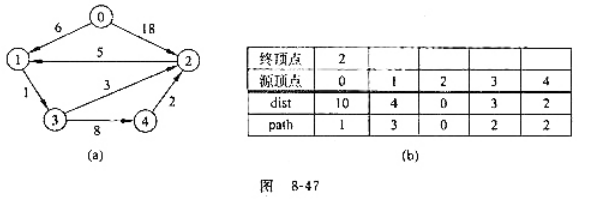
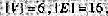则G是().
